Scalars, Vectors, Matrices and Tensors

A solid understanding of linear algebra is essential for better comprehension and effective implementation of neural networks.

Getting started with deep learning libraries such as TensorFlow and PyTorch in a "black-box" manner is relatively easy, thanks to the abundance of tutorials and guides available. However, to truly grasp how neural networks work internally and to understand research papers in the field, we must become comfortable with the underlying mathematics, particularly linear algebra, probability, and calculus, that form the foundation of neural networks.

In this article, I’ll cover the fundamentals of linear algebra: scalars, vectors, matrices, and tensors.

Scalars

Scalars are the physical quantities that are described by magnitude only. In other words, scalars are those quantities that are represented just by their numerical value. Examples include volume, density, speed, age, etc. Scalar variables are denoted by ordinary lower-case letters (e.g., \(x, y, z\)). The continuous space of real-value scalars is denoted by \(\mathbb{R}\). For a scalar variable, the expression x∈\(\mathbb{R}\) denotes that \(x\) is a real value scalar.

Mathematical notation: \(a\epsilon\mathbb{R}\), where \(a\) is learning rate

Vectors

A vector is an array of numbers or a list of scalar values. The single values in the array/list of a vector are called the entries or components of the vector. Vector variables are usually denoted by lower-case letters with a right arrow on top (\(\overset{\rightarrow}{x}, \overset{\rightarrow}{y}, \overset{\rightarrow}{z}\)) or bold-faced lower-case letters (x, y, z).

Mathematical notation: \( \overset{\rightarrow}{x}\epsilon \mathbb{R}^{n} \), where \(x\) is a vector. The expression says that the vector \(\overset{\rightarrow}{x}\) has \(n\) real-value scalars.

\[ \overset{\rightarrow}{x} = \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ .\\ .\\ x_{n} \end{bmatrix} \]

where \(x_{1}, x_{2}, ..., x_{n}\) are the entries/components of the vector \(\overset{\rightarrow}{x}\).

A list of scalar values, concatenated together in a column (for the sake of representation), becomes a vector.

Creating vectors in NumPy:

#loading numpy
import numpy as np

# creating a row vector
row_v = np.array([1, 2, 3])

#creating a column vector
column_v = np.array([[1],
                     [2],
                     [3]])

Matrices

Like vectors generalize scalars from order zero to order one, matrices generalize vectors from order one to order two. In other words, Matrices are 2-D arrays of numbers. They are represented by bold-faced capital letters (\(A, B, C\)).

Mathematical notation: \(A\epsilon \mathbb{R}^{m*n}\) means that the matrix \(A\) is of size \(m*n\) where \(m\) is rows and \(n\) is columns.

Visually, a matrix \(A\) with size \(3*4\) can be illustrated as:

\[ A = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix} \]

Creating matrices in NumPy:

# Creating a 3*3 matrix
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])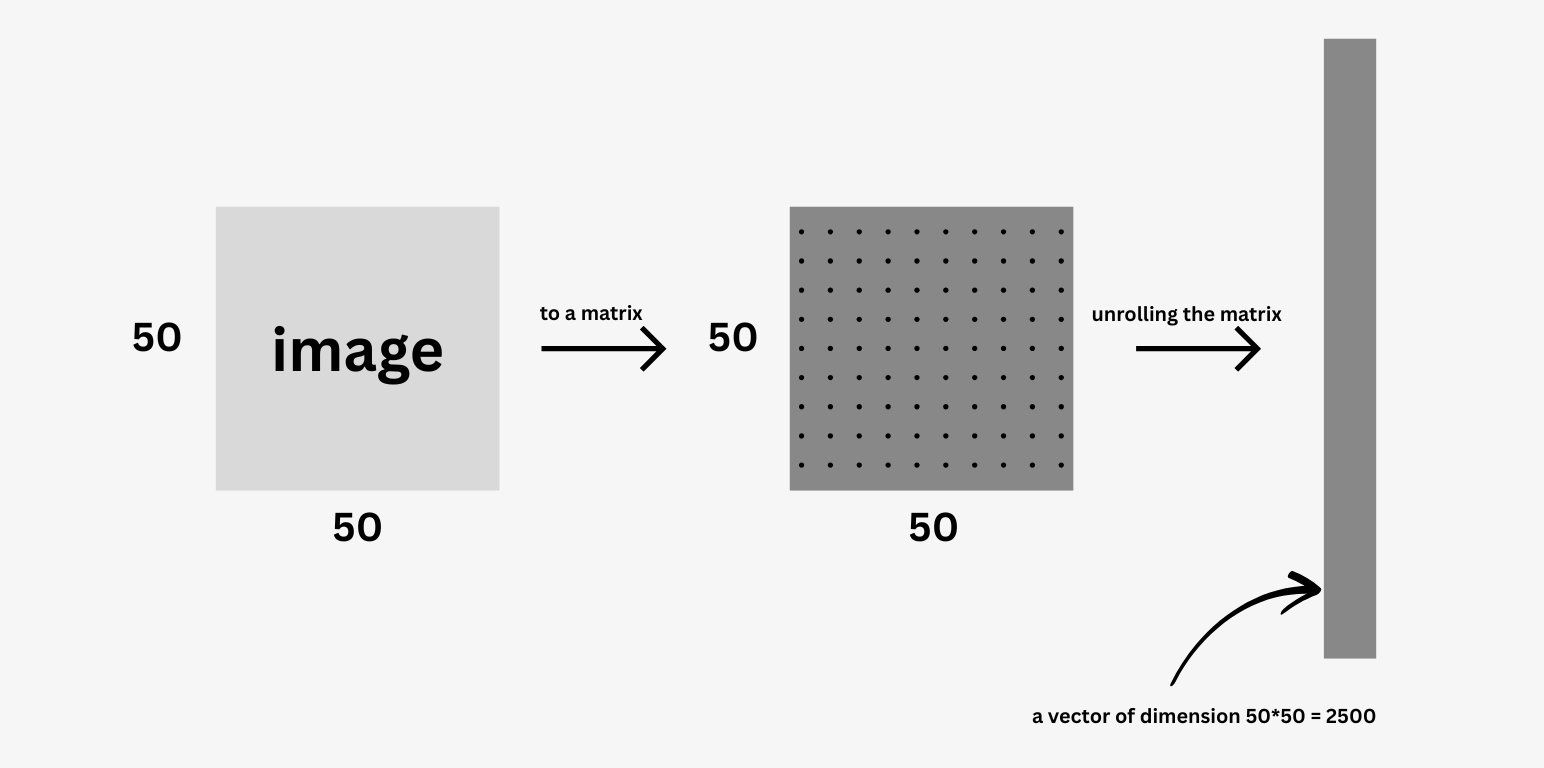

Real-world use case: The learning algorithms need numbers to work on. Data such as images have to be converted to an array of numbers before the data is fed to the algorithms. In the above illustration, an image of 50*50 is first converted to a 50*50 matrix. Here we are supposing that the image is grayscale. Thus the value of a pixel ranges from 0 to 255. The resulting image is then converted to a vector of dimension 2500. This way an image is converted to a vector.

Tensors

Tensors can be simply understood as an n-dimensional array with n greater than 2. Vectors are first-order tensors, and matrices are second-order tensors.

The mathematical notation of tensors is similar to that of matrices. Only the number of letters that define the dimension is greater than two. \(A_{i,j,k}\) defines a tensor \(A\) with \(i,j,k\) dimensions.

Creating a Tensor in NumPy:

tensor = np.array([
  [[1,2,3],    [4,5,6],    [7,8,9]],
  [[10,11,12], [13,14,15], [16,17,18]]
  [[19,20,21], [22,23,24], [25,26,27]],
  ])

We’ll be dealing with tensors while working with color image and video data. When a color image is converted to an array of numbers the dimension will be something like height, width and color axis. The color axis basically defines a different set of numbers for Red-Green-Blue channels. For each color channel, we'll be creating a matrix based on the pixel value. Then the resulting matrices are unrolled to form a vector.

Final thoughts:

We saw how vectors generalize scalars to a 1-D array, and how matrices generalize vectors to form a 2-D array. One term that is common to scalars, vectors and matrices is "tensor". A scalar is 0^th order tensor, a vector is 1^st order tensor and a matrix is 2^nd order tensor.

This article just scratched the surface of Linear algebra. In my next article, I'll discuss about some important operations that are performed on Scalars, Vectors, Matrices and tensors.

I'll see you guys in the next one.